Индуцированное расслоение
Индуцированное расслоение — расслоение , индуцированное отображением и расслоением , где — подпространство прямого произведения , состоящее из пар , для которых , и .
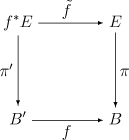
При этом следующая коммутативная диаграмма образует декартов квадрат:
Свойства
[править | править код]- Отображение индуцированного расслоения в исходное расслоение, определённое формулой , является морфизмом расслоений, накрывающим .
- Для каждой точки ограничения на слой является гомеоморфизмами.
- Для любого расслоения и морфизма , накрывающего , существует один и только один морфизм , удовлетворяющий соотношениям
- .
- Расслоения, индуцированные изоморфными расслоениями, изоморфны, расслоение, индуцированное постоянным отображением, изоморфно тривиальному.
- Для любого сечения расслоения отображение , определённое формулой , является сечением индуцированного расслоения и удовлетворяет соотношению .
Литература
[править | править код]Хатчер А. Алгебраическая топология. — М.: МЦНМО, 2011. — 688 с. — ISBN 978-5-94057-748-5.
В статье не хватает ссылок на источники (см. рекомендации по поиску). |
Это заготовка статьи по математике. Помогите Википедии, дополнив её. |